(PRINCIPIO DE ARQUÍMEDES)

El principio de Arquímedes afirma que todo cuerpo sumergido en un fluido experimenta un empuje vertical y hacia arriba igual al peso de fluido desalojado.

La explicación del principio de Arquímedes consta de dos partes como se indica en la figuras:

El estudio de las fuerzas sobre una porción de fluido en equilibrio con el resto del fluido.
La sustitución de dicha porción de fluido por un cuerpo sólido de la misma forma y dimensiones.

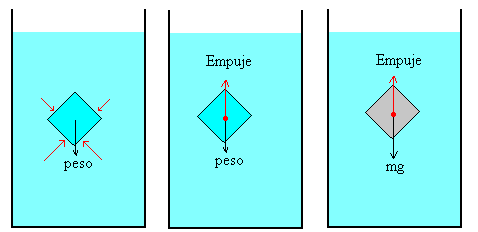
Porción de fluido en equilibrio con el resto del fluido.

Consideremos, en primer lugar, las fuerzas sobre una porción de fluido en equilibrio con el resto de fluido. La fuerza que ejerce la presión del fluido sobre la superficie de separación es igual a p·dS, donde p solamente depende de la profundidad y dS es un elemento de superficie.

Puesto que la porción de fluido se encuentra en equilibrio, la resultante de las fuerzas debidas a la presión se debe anular con el peso de dicha porción de fluido. A esta resultante la denominamos empuje y su punto de aplicación es el centro de masa de la porción de fluido, denominado centro de empuje.

De este modo, para una porción de fluido en equilibrio con el resto, se cumple

Empuje=peso=r_f·gV

El peso de la porción de fluido es igual al producto de la densidad del fluido r_f por la aceleración de la gravedad g y por el volumen de dicha porción V.

Se sustituye la porción de fluido por un cuerpo sólido de la misma forma y dimensiones.

Si sustituimos la porción de fluido por un cuerpo sólido de la misma forma y dimensiones. Las fuerzas debidas a la presión no cambian, por tanto, su resultante que hemos denominado empuje es la misma y actúa en el mismo punto, denominado centro de empuje.

Lo que cambia es el peso del cuerpo sólido y su punto de aplicación que es el centro de masa, que puede o no coincidir con el centro de empuje

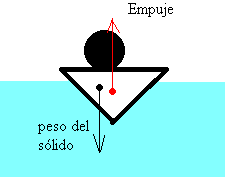
Por tanto, sobre el cuerpo actúan dos fuerzas: el empuje y el peso del cuerpo, que no tienen en principio el mismo valor ni están aplicadas en el mismo punto.En los casos más simples, supondremos que el sólido y el fluido son homogéneos y por tanto, coinciden el centro de masa del cuerpo con el centro de empuje.

En ese tiempo, Arquímedes era un sabio muy respetado y llego a ser consejero del rey. Este se mandó a hacer una corona de oro, pero desconfió del herrero que le hizo el trabajo y le pidió a Arquímedes que resolviera su duda. Pasaron los días y no se encontraba respuesta, entonces el rey, furioso, le grito: ¡Si no resuelves mi duda te corto la cabeza!

Muy desanimado y triste, Arquímedes fue a su casa a darse un baño para relajarse. Pensado en que iba a morir, observo el agua de la tina y se sumergió de nuevo, observando el mismo fenómeno. Luego introdujo varios objetos al agua, cada objeto que introducía flotaba o se sumergía por completo cambiando el nivel del agua de la tina.

¡Eureka!, dijo con alegría, y salió corriendo por toda Siracusa para llegar al palacio real. Una vez ahí utilizo sus observaciones para resolver la duda del rey.

El PRINCIPIO DE BERNOULLI

TEOREMA DE DANIEL BERNOULLI

El teorema de Bernoulli es también conocido como el teorema de trabajo-energía en los fluidos.

"En un líquido estacionario, la suma de las energías cinéticas, potencial y de presión en la misma en cualquier parte del fluido"

En dinámica de fluidos, el principio de Bernoulli, también denominado ecuación de Bernoulli o trinomio de Bernoulli, describe el comportamiento de un fluido moviéndose a lo largo de una corriente de agua. Fue expuesto por Daniel Bernoulli en su obra Hidrodinámica (1737) y expresa que en un fluido ideal (sin viscosidad ni rozamiento) en régimen de circulación por un conducto cerrado, la energía que posee el fluido permanece constante a lo largo de su recorrido. Considera que en una tubería que posee una elevación, la presión es menor en la parte más alta.

Cinética: es la energía debida a la velocidad que posea el fluido.
Potencial gravitacional: es la energía debido a la altitud que un fluido posea.
Energía de flujo: es la energía que un fluido contiene debido a la presión que posee.

La siguiente ecuación conocida como “Ecuación de Bernoulli” (Trinomio de Bernoulli) consta de estos mismos términos.

$ \frac{V^2 \rho}{2}+{P}+{\rho g z}=constante $

donde:

$V$ = velocidad del fluido en la sección considerada.
$\rho$ = densidad del fluido.
$P$ = presión a lo largo de la línea de corriente.
$g$ = aceleración gravitatoria
$z$ = altura en la dirección de la gravedad desde una cota de referencia.

Para aplicar la ecuación se deben realizar los siguientes supuestos:

Viscosidad (fricción interna) = 0 Es decir, se considera que la línea de corriente sobre la cual se aplica se encuentra en una zona ‘no viscosa’ del fluido.
Caudal constante
Flujo incompresible, donde ρ es constante.
La ecuación se aplica a lo largo de una línea de corriente o en un flujo rotacional

Aunque el nombre de la ecuación se debe a Bernoulli, la forma arriba expuesta fue presentada en primer lugar por Leonhard Euler.

Un ejemplo de aplicación del principio lo encontramos en el flujo de agua en tubería.

Cada uno de los términos de esta ecuación tiene unidades de longitud, y a la vez representan formas distintas de energía; en hidráulica es común expresar la energía en términos de longitud, y se habla de altura o cabezal, esta última traducción del inglés head. Así en la ecuación de Bernoulli los términos suelen llamarse alturas o cabezales de velocidad, de presión y cabezal hidráulico, del inglés hydraulic head; el término $z$ se suele agrupar con $P/\gamma$ (donde $\gamma = \rho g$ ) para dar lugar a la llamada altura piezométrica o también carga piezométrica.[editar]Características y consecuencia

También podemos reescribir este principio en forma de suma de presiones multiplicando toda la ecuación por $\gamma$ , de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.

$\underbrace{\frac{\rho V^2}{2}}_{\mbox{presión dinámica}}+\overbrace{P+ \gamma z}^{\mbox{presión estática}}=constante$

o escrita de otra manera más sencilla:

$q+p=p_0$

donde

$q=\frac{\rho V^2}{2}$
$p=P+ \gamma z$
$p_0$ es una constante-

Igualmente podemos escribir la misma ecuación como la suma de la energía cinética, la energía de flujo y la energía potencial gravitatoria por unidad de masa:

$\overbrace{\frac{{V}^2}{2}}^{\mbox{energía cinética}}+\underbrace{\frac{P}{\rho}}_{\mbox{energía de flujo}}+\overbrace{g z}^{\mbox{energía potencial}} = constante$

APLICACIÓN DEL PRINCIPIO DE BERNOULLI

Tiene varias aplicaciones en todo lo que es movimiento de fluidos especialmente en tuberías/cañerías.

Permite calcular las velocidades y presiones en distintos tramos, pero además sirve para evaluar las pérdidas de presión, y simular la distribución de caudales (gastos, flujos, en litros /s, m³/s, o por hora, etc.) en cañerías y sistemas hidráulicos con diferencia de diámetros, alturas, distintas obstrucciones al paso del fluido (líquido o gaseoso, o sea neumáticos también).

Una evaluación que suele hacerse es evaluar la fuerza de sustentación sobre las alas de un avión. Se basa en despreciar la diferencia de alturas geométrica entre las caras superior e inferior del ala, pero considerando la diferencia de velocidades y la superficie alar.

Otra aplicación es el tubo Venturi, que sirve para medir caudales y velocidades de fluidos en cañerías por diferencia de presiones entre dos puntos en uno de los cuales hay una restricción a la circulación.

teorema de torricelli

La velocidad del chorro que sale por un único agujero en un recipiente es directamente proporcional a la raíz cuadrada de dos veces el valor de la aceleración de la gravedad multiplicada por la altura a la que se encuentra el nivel del fluido a partir del agujero.

Matemáticamente se tiene:

v = raíz cuadrada ((2 * g) * (h))

Ejemplo de aplicación del teorema de Torricelli (vaciado de un recipiente):

Un depósito cilíndrico, de sección S1 tiene un orificio muy pequeño en el fondo de sección S2 mucho más pequeña que S1 :

Aplicamos el teorema de Bernoulli suponiendo que la velocidad del fluido en la sección mayor ,

Aplicamos el teorema de Bernoulli suponiendo que la velocidad del fluido en la sección s1 es despreciable, v1 es más o menos 0 comparada con la velocidad del fluido v2 en la sección menor s2.

Por otra parte , el elemento de fluido delimitado por las secciones S1 y S2 esta en contacto con el aire a la misma presión, luego p1=p2=p0.

Finalmente, la diferencia entre alturas y1- y2 = H. siendo H la altura de la columna del fluido.

La ecuación de Bernoulli:

Con los datos del problema se escribirá de una forma más simple:

Physical Two

Bienvenidos

martes, 1 de marzo de 2016

UNIDAD 3 :PRINCIPIO DE ARQUIMEDES

TEOREMA DE DANIEL BERNOULLI

Cinética: es la energía debida a la velocidad que posea el fluido.

Potencial gravitacional: es la energía debido a la altitud que un fluido posea.

Energía de flujo: es la energía que un fluido contiene debido a la presión que posee.

La siguiente ecuación conocida como “Ecuación de Bernoulli” (Trinomio de Bernoulli) consta de estos mismos términos.